Breadth-First Search(BFS) & Depth-First Search(DFS)

Breadth-First Search (BFS) is a fundamental algorithm used in computer science for traversing or searching tree or graph data structures. Starting from a selected node, BFS explores all its neighboring nodes at the present depth level before moving on to nodes at the next depth level. This method is particularly useful for finding the shortest path in unweighted graphs.

Algorithm

The BFS algorithm works as follows:

1. Initialization:
→ Start by putting the initial node into a queue.
→ Mark this node as visited.

2. Loop:
→ Remove the front node from the queue and check all its neighbors.
→ If a neighbor hasn't been visited yet, mark it as visited and add it to the queue.
→ Repeat until the queue is empty.

Example: BFS on Our Graph

To better understand BFS, let's walk through the algorithm step-by-step using our graph. We will start from node 8.

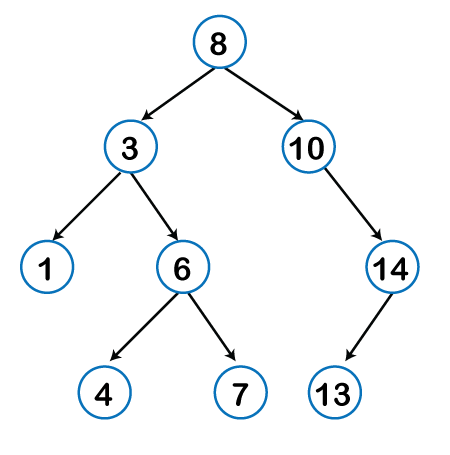
1. Start: Queue = [8], Visited = {8}
2. Process 8: Queue = [], Visited = {8}
→ Add neighbors of 8 to Queue: [3, 10]
3. Process 3: Queue = [10], Visited = {8, 3}
→ Add neighbors of 3 to Queue: [10, 1, 6]
4. Process 10: Queue = [1, 6], Visited = {8, 3, 10}
→ Add neighbors of 10 to Queue: [1, 6, 14]
5. Process 1: Queue = [6, 14], Visited = {8, 3, 10, 1}
→ 1 has no new neighbors
6. Process 6: Queue = [14], Visited = {8, 3, 10, 1, 6}
→ Add neighbors of 6 to Queue: [14, 4, 7]
7. Process 14: Queue = [4, 7], Visited = {8, 3, 10, 1, 6, 14}
→ Add neighbors of 14 to Queue: [4, 7, 13]
8. Process 4: Queue = [7, 13], Visited = {8, 3, 10, 1, 6, 14, 4}
→ 4 has no new neighbors
9. Process 7: Queue = [13], Visited = {8, 3, 10, 1, 6, 14, 4, 7}
→ 7 has no new neighbors
10. Process 13: Queue = [], Visited = {8, 3, 10, 1, 6, 14, 4, 7, 13}
→ 13 has no new neighbors

Applications

→ Shortest Path in Unweighted Graph: BFS is ideal for finding the shortest path in an unweighted graph, as it explores all nodes at the present depth level before moving on.
→ Web Crawlers: BFS can be used by web crawlers to traverse websites layer by layer.
→ Network Broadcasting: In networking, BFS can help in broadcasting a message from a source node to all other nodes.
→ Social Networks: BFS can be used to find the shortest connection path between users in social networks.

Advantages and Disadvantages

Advantages

→ Simplicity: BFS is easy to understand and implement.
→ Shortest Path: Guarantees the shortest path in an unweighted graph.
→ Layer-Wise Traversal: Explores nodes layer by layer, making it useful for problems that require level order traversal.

Disadvantages

→ Memory Usage: Can be memory intensive, as it needs to store all nodes at the present level before moving deeper.
→ Not Suitable for Weighted Graphs: BFS does not work well with weighted graphs where finding the shortest path requires considering edge weights.

Depth-First Search (DFS) is another fundamental algorithm used in computer science for traversing or searching tree or graph data structures. Unlike BFS, DFS starts at the root node and explores as far down a branch as possible before backtracking. This method is particularly useful for solving puzzles and exploring all possible solutions.

Algorithm

The DFS algorithm works as follows:

1. Initialization:
→ Start by putting the initial node into a stack.
→ Mark this node as visited.

2. Loop:
→ Pop the top node from the stack and check all its neighbors.
→ If a neighbor hasn't been visited yet, mark it as visited and push it onto the stack.
→ Repeat until the stack is empty.

Example: DFS on Our Graph

To better understand DFS, let's walk through the algorithm step-by-step using our graph. We will start from node 8.

1. Start: Stack = [8], Visited = {8}
2. Process 8: Stack = [], Visited = {8}
→ Add neighbors of 8 to Stack: [10, 3]
3. Process 3: Stack = [10], Visited = {8, 3}
→ Add neighbors of 3 to Stack: [10, 6, 1]
4. Process 1: Stack = [10, 6], Visited = {8, 3, 1}
→ 1 has no new neighbors
5. Process 6: Stack = [10], Visited = {8, 3, 1, 6}
→ Add neighbors of 6 to Stack: [10, 7, 4]
6. Process 4: Stack = [10, 7], Visited = {8, 3, 1, 6, 4}
→ 4 has no new neighbors
7. Process 7: Stack = [10], Visited = {8, 3, 1, 6, 4, 7}
→ 7 has no new neighbors
8. Process 10: Stack = [], Visited = {8, 3, 1, 6, 4, 7, 10}
→ Add neighbors of 10 to Stack: [14]
9. Process 14: Stack = [], Visited = {8, 3, 1, 6, 4, 7, 10, 14}
→ Add neighbors of 14 to Stack: [13]
10. Process 13: Stack = [], Visited = {8, 3, 1, 6, 4, 7, 10, 14, 13}
→ 13 has no new neighbors

Applications

→ Path Finding: DFS is useful for finding a path from the start node to the goal node.
→ Topological Sorting: DFS is used to perform a topological sort in a directed acyclic graph.
→ Puzzles: DFS is used in puzzles and games that require searching all possible solutions.

Advantages and Disadvantages

Advantages

→ Memory Efficient: DFS requires less memory than BFS as it only needs to store the nodes on the current path.
→ Path Finding: DFS can find a path without needing to explore all nodes at the current depth level.

Disadvantages

→ Can Get Stuck: DFS can get stuck in deep paths if there is a cycle, leading to infinite loops unless handled properly.
→ Not Optimal for Shortest Path: DFS does not guarantee the shortest path in an unweighted graph.