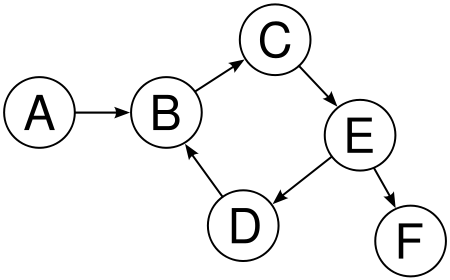
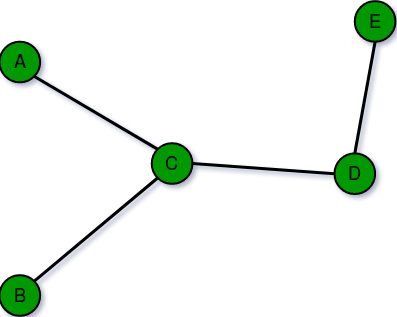
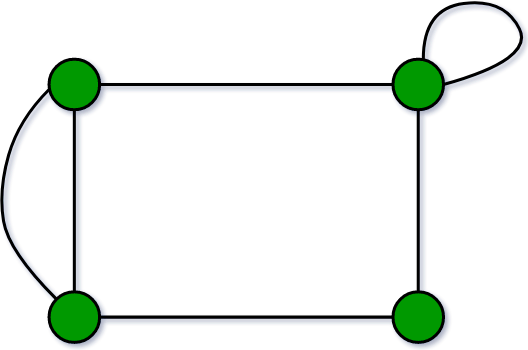
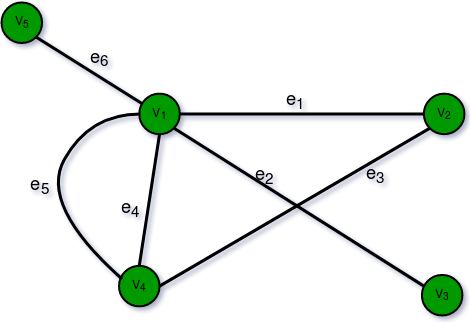
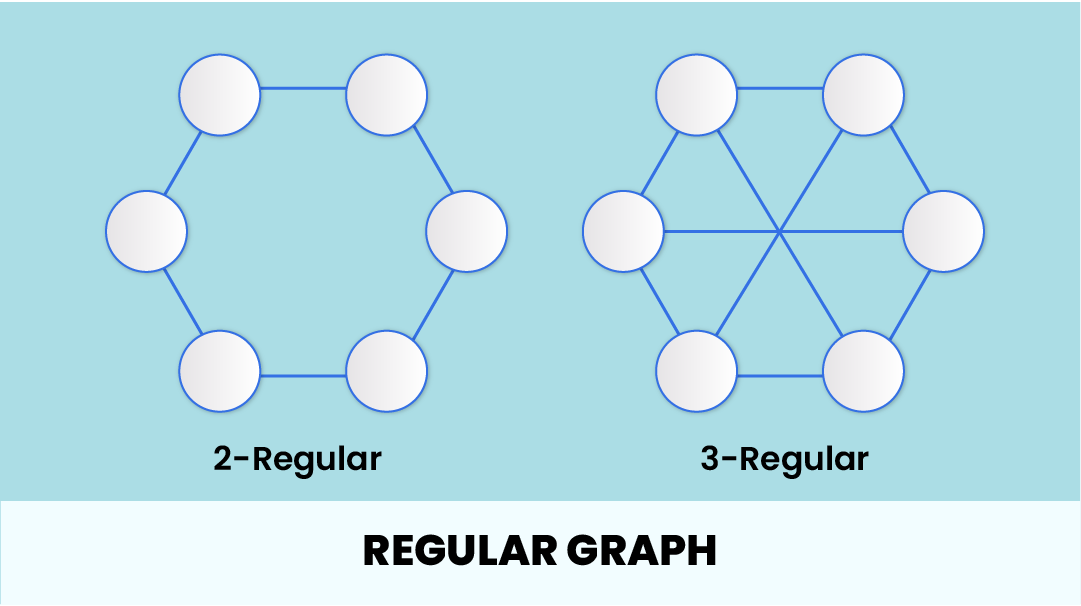
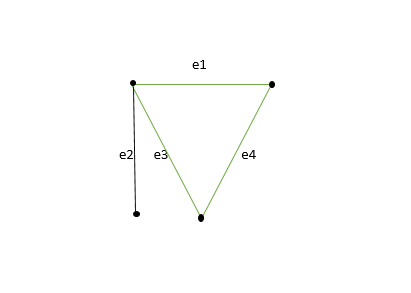
Graph: A collection of nodes (also called vertices) and edges connecting pairs of nodes, used to represent relationships or connections in a network.
Edge (E ): A connection or link between two nodes in a graph.
Node or Vertex (V ): An individual element or point in a graph that can be connected to other nodes via edg
Subgraph: A subset of a graph's nodes and edges that forms a graph on its own.

Degree: The degree of a vertex in a graph is the number of edges connected to it.

Path: A path in a graph is a sequence of vertices connected by edges, where each edge is traversed once. A simple path does not repeat any vertices or edges.
Cycles: A graph with at least one cycle or a path that starts and ends at the same vertex without repeating any edges or vertices.
Tree and its properties
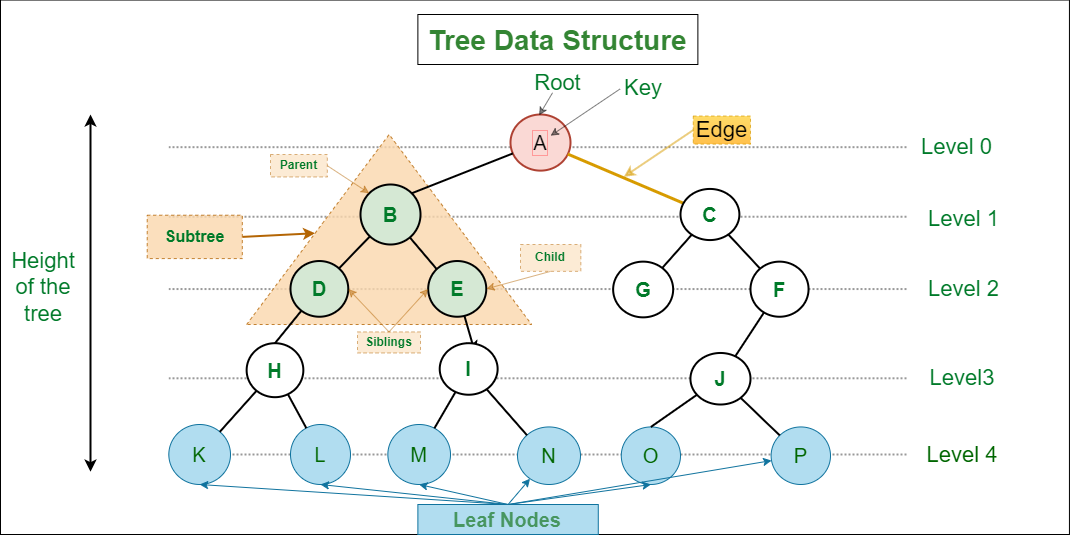
A Tree is a non-linear data structure and a hierarchy consisting of a collection of nodes such that each node of the tree stores a value and a list of references to other nodes (the “children”).
Some important properties of tree data structure:
- Root: The topmost node in a tree, with no parent.
- Key: The value stored in a node.
- Edge: A connection between two nodes.
- Parent: A node that has one or more children.
- Subtree: A tree consisting of a node and all its descendants.
- Child: A node directly connected to another node when moving away from the root.
- Siblings: Nodes that share the same parent.
- Leaf Nodes (Leaves): Nodes with no children.
- Height of Tree: The length of the longest path from the root to a leaf.
- Levels: The level of a node is the number of edges from the root to that node. The root is at level 0.
Some more important tree types:
Binary Search Tree - It is a node-based binary tree data structure that has the following properties:
→ The left subtree of a node contains only nodes with keys lesser than the node’s key.
→ The right subtree of a node contains only nodes with keys greater than the node’s key.
→ The left and right subtree each must also be a binary search tree.
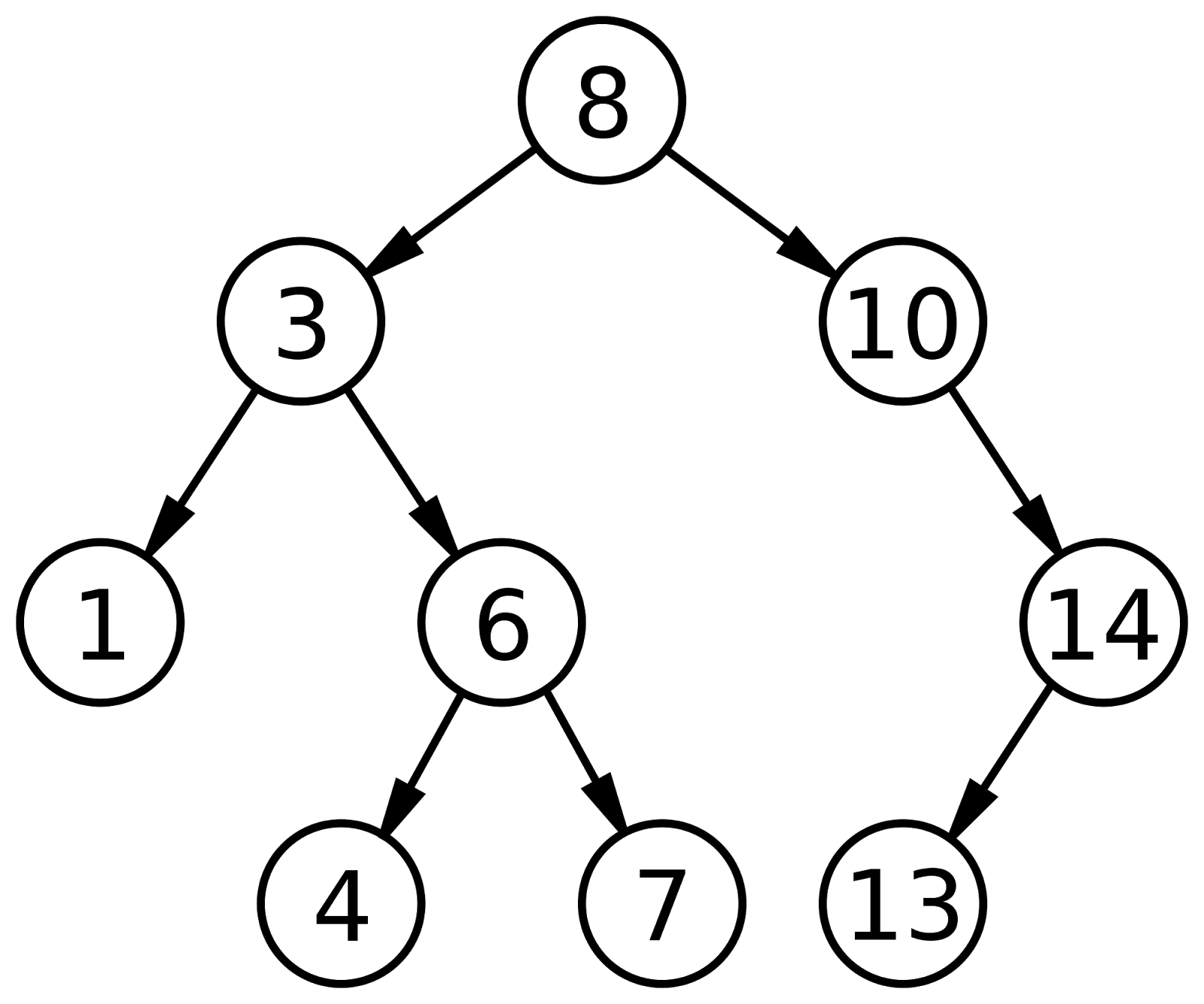
AVL Tree - It is a self-balancing Binary Search Tree (BST) where the difference between heights of left and right subtrees cannot be more than one for all nodes.

Red Black Tree - It is a kind of self-balancing binary search tree where each node has an extra bit, and that bit is often interpreted as the color (red or black). These colors are used to ensure that the tree remains balanced during insertions and deletions.

B-tree - A B-tree is a self-balancing tree data structure designed for handling large datasets efficiently. It maintains sorted data, with each node capable of holding multiple keys and children. By ensuring that all leaf nodes are at the same level and minimizing disk accesses, B-trees provide fast search, insertion, and deletion operations, making them ideal for use in databases and file systems.
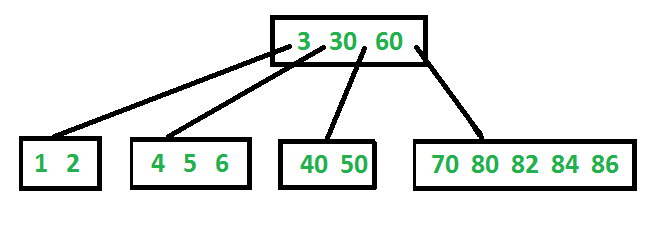
B+ tree - In a B+ tree, all data is stored in the leaf nodes, while internal nodes are used solely for indexing and routing purposes. This design ensures that all leaf nodes are at the same level, simplifying traversal and range queries.